 カメオはドーナツ売りの爺さんに勝負を持ちかけた。彼の提案したルールは次の通りである。
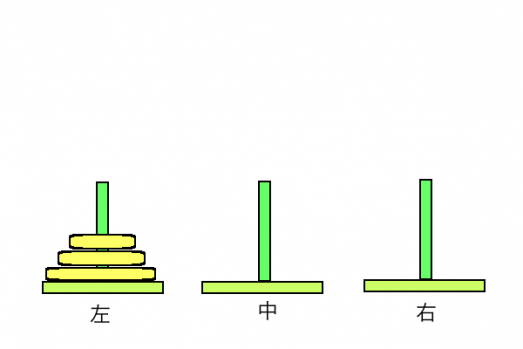
カメオはドーナツ売りの爺さんに勝負を持ちかけた。彼の提案したルールは次の通りである。・ここに3本の杭と、中央に穴の空いた大きさの異なる3枚の円盤(便宜上、A>B>Cとする)がある。
・最初はすべての円盤が、左端の杭に、小さいものが上になるように順に積み上げられている。
・円盤を一回に一枚ずつどれかの杭に移動させることができる。ただし、小さな円盤の上に大きな円盤を乗せることはできない。
以上のルールに則り、すべての円盤を右端の杭に移動させられれば完成だ。
完成までにかかる手数の少ない方が勝利となる。
ルールを聞いた爺さんはすぐさま、最小回数は7回だと答えた。
カメオは爺さんの答えを念押しして、勝負の成立を確認した。
そして彼は、ルールに則り円盤を動かし、最小回数で爺さんに勝利した。
さて、カメオが円盤を移動するのにかかった最小回数は何回か、彼が取った方法を明らかにしつつ答えよ。
【新・形式】【時間制限:6時間】【闇スープ】

ありがとうございました

杭を抜いて一番下を取って移動させることで3回で終わりましたか?

yesno! 3回はyes 杭は抜いていません。 [良い質問]

ドーナツを利用しますか? [編集済]

no 使えません

BとCを杭に通さずにどっか適当なところにどかして、A→B→Cと右に通して5回です。

no

A右B真ん中A真ん中C右A左B右A右ですか?

no 回数と方法を書いてください。それだと7回だと思います。

杭を自由に動かせますか?

noです。

0回、円盤の積まれた杭を右端に動かした…?

noです。

カメオはまず左の一番上の小さな円盤(C)を移動させましたか? [編集済]

no [良い質問]

カメオはズルをしましたか?

no ルールには違反していませんが、あるものに細工はしました。 [編集済] [良い質問]

円盤の穴の直径は関係ありますか?

YES! [良い質問]

杭を移動させることはできますか?

noです(後出しでごめんなさい)

ドーナツは重要ですか?

no 円盤とドーナツが似ていたからです。

カメオは7回以下の回数で爺さんに勝利しましたか?

yes [良い質問]

爺さんがドーナツ屋であることは重要ですか?

no 円盤とドーナツが似ていたからです

爺さんは、カメオに提示されたルールの見落としをしていますか?

no カメオに提示されたルールを聞いて、すぐ答えました。

この問題のキモは杭が1,2,3やA,B,Cなどでなく左,中,右と区別されていること。 最小回数は0回。カメオは向こう側に回り込んで「右端の杭」にすべての円盤が乗った状態にした。

no カメオは円盤を1回以上動かしています。

裏から見たら左右が入れ替わるので0回ですか?

no カメオは円盤を1回以上動かしています。

挿絵は実際にカメオと爺さんが使った円盤や杭の状況と一致していますか? [編集済]

YesNo! 挿絵はミスリードですが、大きいものから順に積み重なっているのはyes [良い質問]

彼が勝った最小回数というのは、7回よりも少ないですか?

yes

カメオは6回以下の回数で爺さんに勝利しましたか?(スミマセン12の質問だと7回も含む感じになっちゃったので質問し直します…)

yes

左の一番大きな円盤(A)を持ち上げてまとめて右の杭に移し替えますか?

no 一回に別の杭へ移動できる円盤は一つです

状況は挿絵通りですか?

YesNo! 挿絵はミスリードですが、大きいものから順に積み重なっているのはyes [良い質問]

爺さんは7回でできなかったので7回で移動させることができたカメオの勝ちですか?

no

普通に考えれば最小回数が7回であり、ドーナツ屋の主人は引き分け以上の結果は得られないにも関わらず勝負を受けたことは重要ですか?

no なぜ勝負を引き受けたかは重要ではありません

ずる賢い手を使いましたか?(これって質問ありですかね?無しでしたら無しとお答えしていただきたい) [編集済]

yesno ルールには違反していませんが、まぁ細工しました。 [良い質問]

最初の一手はC(一番小さい円盤)を中か右に移動させますか? [編集済]

no [良い質問]

一回に別の杭に移動させるのは一枚のみというだけなので、カメオは、①左手でCBを持ち上げておいて、右手でAを左から右に移す。②左手でCを持ち上げておいて、右手でBを左から右に移す。③Aを左から右に移す方法により、3回で完成させましたか? [編集済]

yesno 3回はyesですが、その方法ではありません。一回に持ち上げたのは一枚のみ。片手でできます。 [良い質問]

17 円盤の直径は重要ですか?

YES! [良い質問]

まず三枚を順番に取ってから、大きいほうから順番に右端に置きましたか?

no

1回(左と右の杭を入れ替える)ですか? [編集済]

no 杭は入れ替えられません

最小回数は3回。ドーナツで出来た円盤を、Cはそのまま、Bは少し齧ってCより小さくして、Aはかなり齧って齧られたBよりも小さくしたうえで、右の杭に移動させましたか?

no 円盤は食べられません

(確認)カメオの円盤移動回数は0でしたか?

no 一回以上動かしています。

17 27 Aは左から右の杭まで及ぶ直径の巨大な円盤、BとCは挿絵どおりの直径の円盤。したがって、①Cを左から中へ、②Bを左から右へ、③Cを中から右へ動かすことで、3回でしたか? [編集済]

no Aはそこまで巨大である必要はないです。直径は直径でも…

円盤を移動させる際は必ず杭に通さなければなりませんか?

yes 別の杭に通して移動一回とカウントします。

カメオと爺さんの立ってる場所は重要ですか?

no

一番大きなAを取り出して右へ移す→Bを取り出して右へ移す→Cを取り出して右へ移す で三回ですか?

Yes! ではなぜそんなことができたのでしょう? [良い質問]

カメオと爺さんは向かい合っていますか?

yesno 二人の位置は関係ありません。ヒント参照

相手のじいさんがいなくても成立しますか?

yes

カメオが細工したのは円盤ですか?

Yes! [良い質問]

Aの内径>Cの外径でしたか?

Yes! [良い質問]

爺さんがドーナッツ屋さんなのは関係ありますか? [編集済]

no

ヒントより、爺さんは挿絵の状況を前提に解答し、カメオは挿絵とは異なる状況を前提に解答しましたか? [編集済]

yes というより爺さんが即答したので、カメオはしめしめと懐から円盤と杭を取り出し…最小回数を示して勝利しました。 [良い質問]

上にある円盤を抜かして下の円盤をとることは可能でしたか?

yes [良い質問]

円盤にはどでかい穴が空いていて、大きいものは小さいものを通り抜けることができましたか?(aをbc気にせずに抜くことができる的な) [編集済]

Yes!問いに即してまとめてください! [良い質問]

16 カメオが動かした円盤はA,B,Cの内のいずれかだけですか?

yes カメオはA,B,Cの円盤の内いずれか、あるいは全部のみ動かしました。

ドーナツは重要ですか?

no 関係ありませんが、カメオは戦利品として大量のドーナツを獲得しました。

勝負開始時の状態は、挿絵の通りだと思っていいですか?

No! 挿絵はミスリードです。爺さんがルールを聞いて即答、カメオが確認したときが勝負開始なので…なお、先に勝負を提案したのはカメオの方です。 [良い質問]

カメオが細工したのは杭ですか?

No 杭ではなく… [良い質問]

爺さんがルールを聞いて、即答した段階では、杭に円盤を積む前ですか?

Yes! 重要です。 [良い質問]

27 ABCいずれかの直径が、挿絵とは異なりますか?

yes(ミスリード注意)直径は直径でも…

3つ目のルールでの「どれかの杭」を「左中右のうちどれかの杭」として、成立しますか?

yes そう考えてください

3つの円盤の厚みは同じですか?

yes 厚みは同じです。

3つの円盤の穴の大きさは同じですか?

No!! [良い質問]

まだ、杭に円盤を積む前だったので、右に3枚の円盤を積んで、3回ですか?

no 左の杭に三枚積んだ初期状態からスタートです

円盤はいずれも完全な円の形ですか?

yes 完全な円です。

円盤の素材は重要ですか?

yesno FAに直結する細工に、素材はあまり関係ありません。でも、もっと細かく成立させようと+αの細工を施すなら、木だと面倒ですね。
解説には二つ細工されています。
[良い質問]

Cを右→Bを中→Aを右(内径がCの外径より大きいので重ならない)→Cを左→Bを右→Cを右 で6回ですか?

no 内径は重要です。6回ではありません

通常のハノイの塔のルールなら認められない方法ですか?

Yesno ハノイの塔のルールに違反してはいませんが、おそらく通常verと前提が異なるので、認められないでしょう。というのも [良い質問]

図は間違っていますか?

YesNo! 挿絵はミスリードですが、大きいものから順に積み重なっているのはyes [良い質問]

ドーナッツを全部食べて、右の上に巻き○をしましたね?

no ドーナツおいしいです。

問題文の初期状態は挿絵と同じですか?

YesNo! 挿絵はミスリードです。初期状態は挿絵の見た目と異なるでしょう。ですが、大きいものから順に積み重なっているのはyes [良い質問]

円盤の中央にある穴の直径は重要ですか?

Yes!! [良い質問]

杭をもう一本増やして、5手で右端の杭に移動させましたか?

no 杭はルールの通り3本です。

爺さんがドーナツ売りであることはさすがに関係ないですよね?

yes 全く関係ありません。みなさんに突っ込まれています。ごめんなさい…

円盤の穴の大きさは重要ですか?

Yes!!

挿絵にミスリードを誘う要因はありますか?

yes 挿絵通りのイメージだと解けないのではないでしょうか。(これもミスリード注意…かな) [良い質問]

最小回数3回。円盤にはでかい穴が空いていて、大きいものは小さいものを気にせずに通り抜けることができたから、aを右→bを右→cを右 と移動させた。(つまり真ん中のは正直いらなかった) [編集済]

正解です!よろしければ、でかい穴が空いているのに、「積み上げられている」のは、円盤にどんな細工がされているからか、についてもお考えください。 [正解]

カメオは、7回未満の手順で爺さんに勝ちましたか?

yes

爺さんは円盤を動かしましたか?

no 爺さんは触れていません

勝負に使われていた道具は、挿絵の通りのものですか?

no! カメオが用意した特注です。 [良い質問]

カメオはドーナツを使って何かを行ないましたか?

no 勝利の後、カメオは戦利品のドーナツをぱくぱく食べました。

CはB、BはAの上に乗っていますか?

yes 初期状態では、Aの上にB,Bの上にCが乗っております

それぞれの円盤の大きさは、BはAの、CはBの穴の大きさですか? [編集済]

Yes!もう少し細かく答えていただきたいですが、そういうことです! [良い質問]

一番下のAを持ち上げたとき、他の円盤に引っかからずに持ち上げられましたか?

yes もちろん初期状態のままAを持ち上げると引っかかります。ので [良い質問]

移動された円盤は上から小、中、大の順になっていますか?

yesno 完成後の状態であれば、上から小・中・大の順になっています。

杭は左に1本右に2本と三角のようにしてあるので4回です。 [編集済]

no

円盤の分厚さは全て同じですか?

no

あー、重ねなくていいんですね。Cを右→Bを中→Aを右(内径がCの外径より大きいので重ならない)→Bを右 で四回ですか?

no 重ねる(積み上げる)必要があります。初期状態も重なっています。試行も4回ではありません。

26 円盤をABCの順に動かし、三手ですか?

Yes! なぜそんなことができたのでしょう? [良い質問]

4回以上動かしましたか?

no です

右の杭は縦でなく横向きに刺さっているので3回です。

no 向きは縦です。3回はyes [良い質問]

左の杭は上からぶら下がっていますか?

no 下から上に直立(起立)しています。

閉じたり開いたりができる穴でしたか?(そういえば、今って何人正解者さんいますか?)

no 穴のサイズは不動です。(アースさん1名です)

35 72 73 円盤は分解できますか?

no 分解はできません

じいさんがドーナツ売りであることは重要ですか?

no 円盤売りよりはドーナツ売りの方がいいかなって…形似ているし…全く重要ではないです…

64 円盤は向きを工夫することで大きい円盤の穴をすり抜けることができる作りになっているので、大きい円盤から動かすことで3手で移動させることができますか?

正解です!なお、カメオは二つ細工をしました。一つ目は3手で移動させるための穴の細工。二つ目は三枚をきれいに積み上げるための工夫です。後者についてもよければお考えください。 [正解]

(念のため確認)カメオは杭に触れる事はありましたか?

no 杭に触れる必要はありません

杭をひっくり返しますか?

no ひっくり返しません

76 78 ①穴の直径が一番大きいが一番薄いAを右に動かし、②穴の直径が二番目に大きく、二番目に分厚いBを右に、③穴の直径が一番小さいが一番分厚いCを右に動かし三手ですか?

分厚さは関係ありませんが、穴、移動順、3手で正解です!なお、カメオは二つ細工をしました。一つ目は3手で移動させるための穴の細工。二つ目は三枚をきれいに積み上げるための工夫です。後者についてもよければお考えください。 [正解]

斜めにするとギリギリ通れるサイズの穴でしたか?(ありがとうございます。)

no むしろ積み方を工夫しました。

76 Cが一番分厚く、Aが一番薄いですか?

yesno 分厚さは関係ありません。

それぞれの円盤の大きさがBはAの、CはBの穴の大きさなので、A→B→Cの順で取り出して右の杭に移し替えましたか?(3回)

正解です!なお、カメオは二つ細工をしました。一つ目は3手で移動させるための穴の細工。二つ目は三枚をきれいに積み上げるための工夫です。後者についてもよければお考えください。 [正解]

真ん中の杭は使いましたか?

No! [良い質問]

円盤は曲がりますか?

yesno 曲げる必要はありません

カメオの試行回数は5回ですか?

no

イラストと実際の塔に違いはありますか?

yes! 挿絵はミスリードです。大きいものから順に積み上がっているのはyes [良い質問]

輪がドーナツで出来ていましたか?

no 輪は円盤です。

(確認)最終的には右にC→B→Aの順で重なりますか?

yes 上から順に、C→B→Aとなります。

手数というのは円盤の移動だけでなく解答する行為も含まれますか?

No 手数とは、右の塔に、上からC→B→Aの順に重ねたときにかかった、円盤の移動回数のことを指します。その数と、カメオがどんな方法をとったかをお答えください。

杭の位置は移動しましたか?

no 杭の位置は変わりません。

カメオは、円盤を動かす以外の行動を取りましたか?

yesno 最初にカメオは円盤と杭を用意し、初期状態になるよう積みました。その時点で0回。そこからスタート。スタートしてからは、円盤以外には触れていません。 [良い質問]

杭のある場所は重要ですか?

no 特に重要ではありません。

三枚を綺麗に積み上げるための細工も円盤にしましたか?

yes 円盤にしました。それと積み方も工夫しました。

88 円盤の穴をCBAの順に大きくしつつ、それぞれの円盤に開ける穴の位置をずらしてうまく積み上がるようにしましたか? [編集済]

no 穴を開ける位置は中央のみです。

A右B右C右の三回ですか?

yes! なぜそれができたのでしょう? [良い質問]

横に片寄らせて積みましたか?

yes! まあそれだけだと、重心の関係でみっともないことになるので…(引っかかってるだけできれいに積み上がっているとは言い難いので…) [良い質問]

Gさんは口だけで手を動かさず、実際に右端に移動させることはなかった。カメオ「ええんか?本当にそれでええんか?」Gさん「ええよ」 この時点でどれだけ手数をかけようと勝ちは確定だったが、カメオは最小回数7回でゲームに勝利した。 [編集済]

no カメオは7回未満で円盤を動かし、勝っています。まあGさんが「ええよ」っていってくれてカメオは内心ガッツポーズだと思います。

円盤を一回に一枚ずつどれかの杭に移動「させることができる」を「させなくてはいけない」に置き換えてもカメオは勝利できましたか?

yes

初期状態では、左の杭が三枚すべての円盤の穴に刺さっていましたか?

yes

爺さんは即答しただけで実際に円盤を7回動かして完成させたのは彼だから、彼が勝ったのですか?

no 念押しは、爺さんの回答が7回だとお互いに合意を形成するためです。まぁ、実際に動かしたいと言われたらちょっと面倒なことになりましたが…カメオは7回未満で勝ちました。

Cの円盤は実は円筒形ですか? [編集済]

yesno 円柱ではなく、ちょっと分厚い円盤です。でも、円柱でも成立はします

Bの内径>Cの外径ですか?

Yes! [良い質問]

カメオが最初に動かしたのは、一番小さい円盤でしたか?

No [良い質問]

穴とふちの部分をずらして積みましたか? [編集済]

yesno 積み方の工夫では、横に片寄らせて積みました。それだけだとちょっとみっともないので、円盤の方に細工をしました。

カメオの方法はいわゆる「ルールの穴」をつくような方法でしたか?

yesno ルールに違反はしないけど、通常の「ハノイの塔」の答えを出し抜いたので、結果的にはそうですね(うまいので良質) [良い質問]

104穴の直径が上の円盤の大きさより大きかったからですか?

正解です!なお、カメオは二つ細工をしました。一つ目は3手で移動させるための穴の細工。二つ目は三枚をきれいに積み上げるための工夫です。後者についてもよければお考えください。 [正解]

1回の移動とは、ある杭に刺さっている1枚の円盤を、他の杭に刺さった状態にすることですか?

Yes [良い質問]

最小手数は三回ですか?

Yes! どういう順番で、なぜそれができたのでしょう? [良い質問]

カメオは3回動かしましたか?

Yes! どういう順番で、なぜそれができたのでしょう? [良い質問]

左の台の円盤は全て接地しているので、一個ずつ右に移して3回ですか?

yesno(ごめんなさい、全て接地の意味がよくわかりません…1個ずつ右に移して3回はyes!円盤の順番はどうでしょう?)

88 円盤の穴の形を工夫しましたか? [編集済]

yesno 穴の形は円形です。別のところを工夫しました。

爺さんは7回動かし、カメオは1回以上3回以下動かした、という認識で良いですか?

yesno 爺さんは実物を見ることも動かすことなく、7回という答えを提示。それを聞いたカメオは、実際に物を出し、動かして勝ったということです。 [良い質問]

杭を足すことは可能ですか?

no 杭は3本です。

BSはいつ行う予定ですか?

(ネット回線がクソ重でBSの速さについていけないので諦めたよママン…)

88 杭を円錐にしましたか?

no 杭に細工はしていません

円盤をドーナツで代用したのでドーナツを齧り大きさを変えることで7回未満を実現しましたか?

no 円盤はドーナツではありません

左の杭は、上から下に向かって生えていましたか?

no どの杭も、下から上に生えています

下につっかえ棒みたいな支え柱をつけましたか?

no つっかえ棒はありません

ゲームスタート時点で、ハノイの塔の状態は問題文の挿絵に示された状態でしたか?

no 挿絵はミスリードです。爺さんが答えてから、カメオは持参した杭と円盤で初期状態を構築しました。 [良い質問]

円盤は縦方向に重なっておらず、芯を中心とした外側に向かって重なっていて、全てが地面についており外側に行くほど低く小さくなっている。なので、芯に近い方から一個ずつ右に抜いて移して3回 ですか?

no 円盤は縦方向に重なっています。そこまで複雑でもありません。スタート時点では、B、cは地面についてません

<答え>5回 「Cを持ったままBを持ってBを中に入れる」→「Cを中に入れる」→「Aを右に入れる」→「Cを持ったままBを持ってBを右に入れる」→「Cを右に入れる」 [編集済]

no 5回ではありません

積み重なった状態でも大きな円盤を取り外す事が可能だったため、三回で移動させることが出来ましたか?

yes!可能な理由はなんでしょう?円盤の順番もお答えください [良い質問]

二人の開始状況は平等でしたか?

yesno 爺さんの言質をとって、カメオは杭と円盤を用意して初期状態を組み立てました [良い質問]

杭の下側から円盤を引き抜くことは可能ですか?

no できません

円盤の種類は重要ですか?

yesno 種類というか、、カメオの特注でした。

爺さんの移動回数は7回で、カメオの回数は7回未満でしたか?

yes 結果的にそういうことです

爺さんがルールだけ聞いて即答した理由は重要ですか? [編集済]

no 理由は特に重要ではありません

<答え>3回 「Cを持ってBを持ってAをドーナツのように口でくわえながら右に入れる」→「Bを右に入れる」→「Cを右に入れる」

3回はyes A、B、Cの順序もyes ただそんな苦しそうにしなくても片手でできます。

杭は円盤を貫通していますか?

yes

カメオの移動回数は7回でしたか?

no

初手で”任意の”円盤1枚を動かせますか?

yesno 動かすだけなら問題ないです(ミスリード注意)なお、別の杭に移動させるときは円盤一つづつです。

Aの内径>Bの外径>Bの内径>Cの外径で、同心円上に重なっていればすとんと落ちてしまうが、軸がぶれていたせいで重なっていた。C→B→Aの順で全て地面につくように右に移し、その後Aの内側からBを持ち上げ、軸をずらしてAの上に乗せ、同じようにCもBに乗せる。台座間移動回数なら計三回。 ですか? [編集済]

ほとんど正解ですが、順序だけ違います。それだと右の杭に移動させたとき、杭が三円の中心に来てしまうため、軸をずらして載せることができません。お手数ですがもう一度!なお、ズラすだけなら別の杭に移動させてないのでルール違反ではありません

3つ重ねたドーナツを一口ずつかじり、下の大きなドーナツからABCの順で右の杭に置いていきましたか? [編集済]

no 円盤はドーナツではありません

<答え>3回 「カメオは爺さんの答えを念押しして」とあることより,カメオは念力の能力を有する事が分かる。よって,「C,Bと順番に宙に浮かせたままAを右に移動させ,B,Cと右に着地させる」ことで完成する。

no カメオにサイコキネシスはできません

円盤の形状は重要ですか?

yes 広い意味では。ただし円盤です。(ミスリード注意) [良い質問]

1回の移動において、最終的な位置を変えなければ、移動対象以外の円盤を動かすことはできますか?

yes!重要です [良い質問]

爺さんがドーナツ売りであることは重要ですか?

no 全く関係ありません。

Aの内径>Bの外径>Bの内径>Cの外径で、同心円上に重なっていればすとんと落ちてしまうが、軸がぶれていたせいで重なっていた。左の台座で一度全てを各円盤の中に落とし、A→B→Cの順で軸をずらしながら重なるように右に移し計三回ですか?

完璧正解です!おめでとうございます! [正解]

円盤は伸縮性がありましたか?

no 伸縮性はありません

動かす順番は「大→中→小」ですか?

yesno 移動させる順番はYes! [良い質問]

円盤には何か特別な仕掛けがありますか?

yes 円盤が特別製です。カメオが細工しています [良い質問]

「小さな円盤の上に大きな円盤を乗せることはできない」とは「Cの上にAを乗せられない」という意味であり、Cの上にBを乗せることは可能ですか?

no cの上にbは乗せられません

実際のハノイの塔のおもちゃで実現可能ですか?(コンピューターなどは除く)

no 市販では無理だと思います(あるかは分かりませんが、) [良い質問]

円盤の形状は変化しますか?

no 変化しません

149より、この問題において「動かす」と「移動させる」は意味が異なりますか?

yes 重要です [良い質問]

円盤はすべて分離していますか?

yes

数学知識は必要ですか?(一応答え確認のため)

no 必要ありません

爺さんは、ハノイの塔を知識として知っていましたか?

yes なので7回と即答しました

円盤を瞬間移動させましたか?

no

「円盤の形状はドーナツ状、かつ円盤は変形したり形を変えたりしないもの」という設定で成立しますか?

yes

杭は本当に3本のみですか?

yes

円盤は本当に3個だけですか?

yes

<答え>3回 一番大きいAを持ってB,Cのバランスを保ちながら右に入れる

no バランスは保ちません

手錠みたいにパカッと開く円盤でしたか?

no 開きません

カメオの提案したルールは、画像通りの状況があることを前提としていますか?

yesno 画像はミスリードありです。カメオの用意した円盤は画像とやや異なります(ミスリード注意) [良い質問]

円盤の素材は重要ですか?

no 正解要素には関係しません

円盤を動かす際には、下にあるものを動かしてもいいですか?

yesno 例えば下の円盤を動かし、上の円盤がズレてしまうのはokです。 [良い質問]

Aの内径>Bの外径、Bの内径>Cの外径となるような円盤でしたか?

yes! [良い質問]

三つの円盤に、穴の大きさと直径以外に違うところはありますか?

bとcにきれいに積み上げるための細工がありますが、faには関係しません [良い質問]

カメオは杭と円盤以外に道具を使いましたか?

no

Aの円盤の穴の直径は、Bの円盤自体の直径よりも小さいですか?

no! [良い質問]

爺さんがドーナツ売りであることは重要ですか?

no

杭を支える台は、三角錐の形をしていますか?

関係ありません

7回よりも少ない移動回数ですか?

yes

お爺さんはルールを正しく理解していますか?

yes

絵に描かれている以外の物は使用してはいけませんか? [編集済]

yes

最小回数を答えるだけでなく実際に動かさないといけないルールですか?

yesno カメオは動かして答えを証明しました

杭を打ち付けた場所が、平らな板の上だとしても成立しますか?

yes

カメオは、勝負の間に三枚の板すべてに触れましたか?

yes [良い質問]

杭は下にも突き出しているので下から挿して3回です。

no 円盤は持ち上げて移動させています

無重力空間での勝負であり、床に打ち付けられた杭から天井に打ち付けられた杭に円盤を移動させると、小さい円盤から大きい円盤へと順に一度ずつ動かすだけで完成させられますか? すなわち、最小回数は3回

3回はyesですが、重力下の出来事です

円盤の、片寄らせてないほうの重さを軽く、もしくは片寄らせるほうを重くしましたか?

お見事! [良い質問]

円盤の最初の移動方向は真上ですか?

yes

円盤の穴の大きさや形は重要ですか?

yes! [良い質問]

150よりその細工とは横から円盤を引き抜くことができるものですか?

no

磁石でくっつけましたか?

重さでした。

カメオは、爺さんの言った通りの最小回数7回でハノイの塔を完成させた上で、爺さんの挑戦を邪魔することで、爺さんの移動回数を8回以上にしましたか?

no 妨害しません

言葉遊びありますか?

noですが、重要な言葉はあります。(多分ミスリードになるかも) [良い質問]

板A,Bに空いた穴はそれぞれ板B,Cよりも大きい大きさになっている。穴をうまくズラすことで、最初は積み重なるような位置に置かれているものの、板をズラして杭から抜き移動させれば、A,B,Cの順に3回移動するだけで完成させられますか?

正解ですね!お見事 [正解]

円盤の材質はゴムで伸縮自在のため、下の円盤の穴に上の円盤を通すかたちで抜き取ることが出来るため、3回で移動を完了しましたか? [編集済]

no ゴムません

Aの穴の大きさがBの円盤の大きさより、Bの穴の大きさがCの円盤の大きさより大きいので、上から見て三重丸みたいな感じになるようにして3回です。

正解です! [正解]

下の円盤の穴が上の円盤の直径より大きいため、下を先に抜き取ることが出来るため、3回で移動を完了しましたか?

正解です! [正解]

167 Aの内径>Bの外径、Bの内径>Cの外径となるような円盤だったため、ABCの順でとりはずし三回で移動することが可能でしたか?

正解です! [正解]
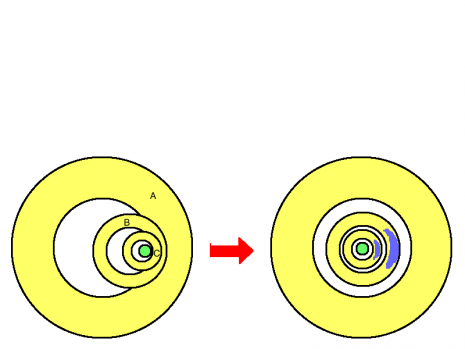
円盤A,Bは、一つ小さい円盤の円周より大きい穴が空いた円盤である。
(円盤Aの穴>円盤Bの円周、円盤Bの穴>円盤Cの円周)
なお、「積み上げられている」状態を正確に表すため、円盤B,円盤Cの片側(右図では青く塗っている箇所)を特に重くするという細工を施した。
初めに、左端の杭に積み上げられている左図の円盤の位置をずらし、右図のようにする。円盤の位置をズラすだけでは、ほかの杭に移動させていないのでルール違反ではない。
次に、Aから順に右端の杭に移動させていき、左図のように積み上げていく。
よって必要な最小手数は3回となる。
こうしてカメオは見事勝利し、大量のドーナツをゲットすることができたのだった。
「Goodスープ認定」はスープ全体の質の評価として良いものだった場合に押してください。(進行は評価に含まれません)
ブックマークシステムと基本構造は同じですが、ブックマークは「基準が自由」なのに対しGoodは「基準が決められている」と認識してください。












