20の扉のスープ【要知識】

下のような20の扉問題が出された。

「あるアルファベット4文字を当てよ。」

その4文字が何を表すかは誰一人知らなかったが、

ちょうど20問目で正解を出すことができたし、正解を出せることをみんな知っていた。

どういうことだろう？

17年06月30日 21:04 [上３]
【ウミガメ】

要知識は「数学」です。電卓を用意しましょう。

No.1[とむわん]06月30日 21:0606月30日 21:07

その20の扉において回数制限は重要ですか？

はい、20回です。 [良い質問]

No.2[QQS]06月30日 21:0806月30日 21:09

アルファベット4文字の特定は必要ですか？

いいえ　不要です [良い質問]

No.3[にのなん]06月30日 21:0806月30日 21:09

問題文中の20問目とは、20回目の質問ということですか？

はい! 誤字でした...

誤字がありました。20問目→20回目の質問です。

No.4[にのなん]06月30日 21:1006月30日 21:10

20問目で正解を出せるように、調整した人物がいますか？

はい！ [良い質問]

No.5[チハ]06月30日 21:1106月30日 21:11

アルファベット4文字の特定は必要ですか？

いいえ

No.6[QQS]06月30日 21:1206月30日 21:13

4　調整した人物は出題者ですか？

いいえ！　質問する側です [良い質問]

No.7[とむわん]06月30日 21:1206月30日 21:14

4は問題の出題者ですか？

いいえ！

No.8[チハ]06月30日 21:1306月30日 21:14

回数制限は20回でしたか？

はい！

No.9[チハ]06月30日 21:1506月30日 21:16

何故調整したかは重要ですか？

はいいいえ！　問題を解くためです [良い質問]

No.10[とむわん]06月30日 21:1606月30日 21:17

正解を出せることはわかっていたものの、正解が何かは最後まで誰もわかりませんでしたか？

いいえ！　わかっていて、実際20回目に正解が出ました。

No.11[チハ]06月30日 21:1706月30日 21:18

出題ルールとして20回目の質問で答えが出た場合にのみ正解を付けますか？

いいえ！　もっと早く正解することもできます。

No.12[QQS]06月30日 21:1806月30日 21:20

質問者は、20個目の質問をした時点でもまだ正解の内容を知らなかったですか？

いいえ！ついに正解にたどり着いたので、20回目の質問で正解できました。 [良い質問]

No.13[とむわん]06月30日 21:2006月30日 21:22

20番目の質問をした人の詳細は重要ですか？

いいえ　誰でもできたはずです

No.14[チハ]06月30日 21:2006月30日 21:22

調整したのは質問者全員ですか？

はい　相談の結果、みんなで調整することになりました。

No.15[チハ]06月30日 21:2106月30日 21:22

確認ラテシンの話ですよね？

はい！　ラテシンです。

No.16[チハ]06月30日 21:2306月30日 21:24

問題を解くために調整は必須ですか？

はいいいえ　調整しなくても正解するかもしれませんが、調整することで確実になります。

No.17[QQS]06月30日 21:2306月30日 21:24

19個目の回答を得た時に正解が分かりましたか？

はい！ [良い質問]

No.18[とむわん]06月30日 21:2306月30日 21:26

出題者に20個全ての質問を答えてもらいたいから、質問数を調整しましたか？

いいえ！　正解にたどり着くためには19回の質問が必要だったのです！ [良い質問]

No.19[さはら]06月30日 21:2406月30日 21:26

その４文字は特定の単語のような、各文字の並び順まで当てる必要のあるものですか？

はいいいえ　並び順は必要ですが… [良い質問]

No.20[チハ]06月30日 21:2606月30日 21:27

今までの質問の中で要知識の内容に関係するものはありましたか？

いいえ　まだありません

30回で出なければ要知識の内容を発表します。

No.21[準鉄]06月30日 21:3006月30日 21:32

スープパートナーは関係ありますか？

いいえ！　関係ありません。

No.22[きのこっこ]06月30日 21:3106月30日 21:32

計算は必要ですか？

はい！　その通りです！ [良い質問]

No.23[準鉄]06月30日 21:3206月30日 21:33

4 出題者の別アカウントが調整しましたか？

いいえ！

要知識は「数学」です。電卓を用意しましょう。

No.24[準鉄]06月30日 21:3406月30日 21:34

闇スープで出題しましたか？

いいえ！

No.25[チハ]06月30日 21:3506月30日 21:36

算数ではなく数学ですか？

はいいいえ　高校で習いますが計算自体は難しくないです。

No.26[さはら]06月30日 21:3506月30日 21:37

4文字中、同じ文字の重複はありますか？

はいいいえ　あってもなくても成立します。

No.27[チハ]06月30日 21:3606月30日 21:39

電卓での計算の結果、アルファベット4文字がわかりますか？

はいいいえ　「アルファベット4文字がわかること」がわかります。 [良い質問]

No.28[flan]06月30日 21:3906月30日 21:40

「AとBですか」「BとCですか」・・・という風に質問していきましたか？

いいえ！　ですが質問のしかたは重要です。

No.29[準鉄]06月30日 21:3906月30日 21:41

特定の時間に質問しますか？

いいえ　いつでもかまいません。

No.30[Litsuki]06月30日 21:4006月30日 21:41

必要な知識は確率ですか？

はいいいえ　近いですが確率というよりは・・・

No.31[flan]06月30日 21:4206月30日 21:44

組み合わせ26C４使いますか？

いいえ！　ですが惜しいです(単に数学の話です)。重複してもいい場合は・・・ [良い質問]

No.32[Litsuki]06月30日 21:4306月30日 21:46

必要な知識は順列ですか？

はい！ [良い質問]

30突破ヒント　アルファベットは26種類です。[編集済]

No.33[Litsuki]06月30日 21:4406月30日 21:46

質問者が調整しなかった場合、20問目までに正解のでる可能性はありましたか？

はい！　ありますが運ゲーです。 [良い質問]

No.34[きのこっこ]06月30日 21:4806月30日 21:49

電卓で26^4を20回2で割ると1以下になりますが、それは重要ですか？

はい！重要です！ [良い質問]

No.35[準鉄]06月30日 21:5406月30日 21:56

一つの文字について5回の質問をすれば必ず分かりますが重要ですか？

はい！　重要な考え方です！ [良い質問]

どういう質問をすれば必ずわかるかをまとめた方を正解とします。

No.36[flan]06月30日 21:5906月30日 22:00

重複組み合わせ29C4ですね？

順番も答える必要があるので重複順列26^4です！ [良い質問]

No.37[QQS]06月30日 21:5906月30日 22:01

34，35より　「1文字目はアルファベット最初の13文字のどれかですか？」のようにして質問枠5つ使って1文字ずつ当てていきましたか？

No! かなり惜しい！ [良い質問]

5回で1文字ずつ当てる場合、はじめて答えがわかるのは「20回目」の質問で、「正解をたずねる質問」ができないのです！！
どうすればいいでしょうか？[編集済]

No.38[QQS]06月30日 22:0706月30日 22:10

15回の質問で3文字目まで特定しましたか？

たぶんはい　(ミスリード注意)

No.39[準鉄]06月30日 22:1006月30日 22:12

アルファベット4つの文字列を辞書に並べ、AAAA〜GKZZの間にあるかを繰り返し聞いていくことで19回で文字を特定できますか？

Yes!!! 完璧です！ [正解]

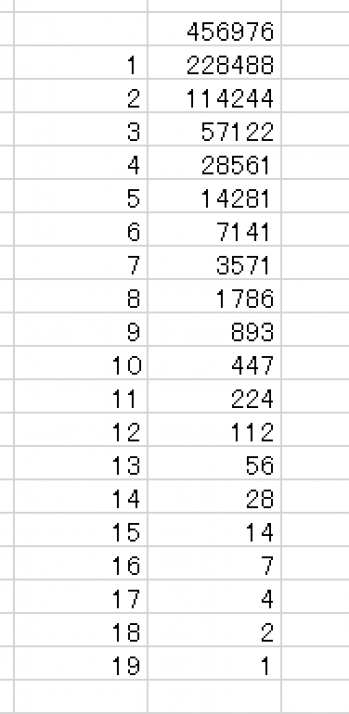
アルファベット4文字の組み合わせの総数は26の4乗=456976通り。

一方、Yes/Noの質問19回で判定できる組み合わせの最大数は2の19乗=524288通り。

よって、0-AAAA, 1-AAABなどのように通し番号を振って「○○番より上ですか?」というような質問で候補を半分ずつ減らしていけば

(ただし、候補の数が奇数の場合は繰り上げになる)最大19回行えば判定でき、

最後の20回目に正解をたずねる質問をすれば、それがどんな4文字であっても必ず答えがわかる。

質問者は相談の結果この解法にたどり着き、安心して質問することができたのだった。

【補足】

ちなみに、通し番号を使わずに1文字ずつ当てようとすると1文字あたり5回の質問が必要なので、ちょうど20問目で「答えが確定」するだけで正解をたずねる質問ができない(!)

つまり、20の扉が20だからこそ成り立つ問題なのです。

17年06月30日 21:04 [上３]

相談チャットです。この問題に関する事を書き込みましょう。

flan＞＞上3さん出題ありがとうございました！[30日22時48分]

とむわん＞＞なるほどー。出題ありがとうございました！[30日22時22分]

準鉄＞＞上3さん出題ありがとうございます。34がナイスですね[編集済] [30日22時20分]

上３＞＞皆さんありがとうございました。無駄にややこしい問題ですみません・・・準鉄さん正解してくださって本当にありがとうございます！[30日22時17分]

waku [★ラテ・ヘイヘ]＞＞上3さん出題ありがとうございました～。準鉄さん正解おめでとうございます！手計算してるうちに終わってましたｗ[30日22時14分]

QQS＞＞なるほどー。なかなか興味深い問題でした。上3さん、出題ありがとうございました。準鉄さん、正解おめでとうございます。[30日22時14分]

QQS＞＞ミスです、スミマセン[編集済] [30日22時07分]

上３＞＞思った以上に数学の問題になってしまい申し訳ありません・・・20の扉が20でないと成立しない問題なんです・・・[30日22時05分]

waku [★ラテ・ヘイヘ]＞＞参加します。よろしくお願いします（ただしパッと思いつかないのでひとまず様子見）[30日21時46分]

上３＞＞すみません、要知識がよくないのはわかっているのですが思いついてしまったもので・・・[30日21時42分]

チハ＞＞高校で習うだと……中学生の俺には無理ゲーや………()[30日21時38分]

Litsuki＞＞参加します。よろしくお願いします！[30日21時38分]

flan＞＞参加します。[30日21時38分]

きのこっこ＞＞参加します！[30日21時30分]

準鉄＞＞参加します[30日21時29分]

チハ＞＞あばー！なんか既出の質問ばかりすみません…(´・ω・｀)[30日21時14分]

上３＞＞皆様よろしくおねがいします。何の知識が要るかはそのうち明らかになるはずです。[30日21時12分]

チハ＞＞参加させていただきますー！[30日21時11分]

QQS＞＞参加します。宜しく御願いします。[30日21時07分]

とむわん＞＞参加します。[30日21時05分]

ゲストの方は発言できません、ログインまたは登録してください。

Goodスープ認定
「Goodスープ認定」はスープ全体の質の評価として良いものだった場合に押してください。（進行は評価に含まれません）
ブックマークシステムと基本構造は同じですが、ブックマークは「基準が自由」なのに対しGoodは「基準が決められている」と認識してください。